Difference between revisions of "Digital Electronics"
m (→Other Videos) |
|||
| (30 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
A digital circuit is constructed from logic gates. Each logic gate performs a function of boolean logic based on its inputs, such as AND or OR. | |||
Each circuit can be represented as a Boolean Algebra expression; | |||
this topic is an extension of the topic of [[Boolean Algebra]], which includes | |||
a thorough description of truth tables and simplifying expressions. | |||
= Definitions = | = Definitions = | ||
The following table illustrates all logic gates. For each logic gate, the | |||
table shows the equivalent Boolean algebra expression and truth table. | |||
{| class="wikitable" style="text-align: left" | |||
|- | |- | ||
!'''NAME''' | !'''NAME''' | ||
| Line 26: | Line 32: | ||
!'''NOT''' | !'''NOT''' | ||
| [[File:Not-gate-en.svg|128px]] | | [[File:Not-gate-en.svg|128px]] | ||
| X = <math>\overline{A}</math> | | X = <math>\overline{A}</math> or <math>\neg A</math> | ||
| | | | ||
{| class="wikitable" style="text-align: center" | {| class="wikitable" style="text-align: center" | ||
| Line 159: | Line 165: | ||
| 1 || 1 || 1 | | 1 || 1 || 1 | ||
|} | |} | ||
|} | |||
Note that there is some ambiguity in the conversion from a diagram to a circuit. For example, is <math>\overline{A+B}</math> an OR gate followed by a NOT gate, or smply | |||
a NOT gate. | |||
=Online Tools= | |||
| | The [http://www.cburch.com/logisim/index.html Logisim] application is a wonderful tool | ||
for exploring this topic. | |||
Logisim is free to download and use; among its many features is support to automatically draw | |||
a circuit from a Boolean Algebra expression; to simulate the circuit with arbitrary inputs; | |||
and to complete a truth table for the circuit. From the application, you can import the circuit corresponding to the [[#Sample_Problem_1|Sample Problem 1]] | |||
from the file located at [http://www.acsl.org/misc/wiki-digital-electronics-sample1.circ http://www.acsl.org/misc/wiki-digital-electronics-sample1.circ]. | |||
There are many YouTube videos that show how to use the Logisim application; including a very nice [https://www.youtube.com/watch?v=cMz7wyY_PxE 4 minute tutorial]. | |||
Logisim contains many | |||
additional advanced features that are beyond | |||
the scope of ACSL problems. | |||
= Sample Problems = | =Sample Problems = | ||
== Sample Problem 1 == | == Sample Problem 1 == | ||
Find all ordered | Find all ordered triplets (A, B, C) which make the following circuit FALSE: | ||
[[File: | ::[[File:NotABorC.svg|200px]] | ||
'''Solution:''' | '''Solution:''' | ||
This circuit | One approach to solving this problem is to reason about that inputs and outputs are necessary at each gate. For the circuit to be FALSE, both inputs to the file OR gate must be false. Thus, input C must be FALSE, and the output of the NAND gate must also be false. The NAND gate is false only when both of its inputs are TRUE; thus, inputs A and B must both be TRUE. The final answer is (TRUE, TRUE, FALSE), or (1, 1, 0). | ||
Another approach to solving this problem is to translate the circuit into a Boolean Algebra expression and simplify | |||
the expression using the laws of Boolean Algebra. This circuit translates to the Boolean expression <math>\overline{AB}+C</math>. | |||
To find when this is FALSE we can equivalently find when the <math>\overline{\overline{AB}+C}</math> is TRUE. | |||
The expression becomes <math>\overline{\overline{AB}}\cdot \overline{C}</math> after applying DeMorgan’s Law. The double NOT over the AB expression | |||
cancels out, to become <math>AB\overline{C}</math>. The AND of 3 terms is TRUE when each term is TRUE, or A=1, B=1 and C=0. | |||
== Sample Problem 2 == | |||
How many ordered 4-tuples (A, B, C, D) make the following circuit TRUE? | |||
::[[File:circuit-sample2.svg |400px]] | |||
'''Solution:''' | |||
We'll use a truth table to solve this problem. The rows in the truth table will correspond to all possible inputs - 16 in this case, since there are 4 inputs. The output columns will be the output of each gate, other than the NOT gates. The diagram below labels each of the gates; it's useful to keep the column straight when working the truth table. | |||
::[[File:circuit-sample2-labels.svg |300px]] | |||
{| class="wikitable" style="text-align: center" | {| class="wikitable" style="text-align: center" | ||
|- | |- | ||
|colspan="4" style="background-color: #cceeff; font-size: x-small" "|INPUT | |||
|colspan="5" style="background-color: #cceeff; font-size: x-small" "|OUTPUT | |||
|- | |- | ||
| | !rowspan="2" | A | ||
| | !rowspan="2" | B | ||
| | !rowspan="2" | C | ||
| | !rowspan="2" | D | ||
! p | |||
! q | |||
! r | |||
! s | |||
! t | |||
|- | |- | ||
!<math>\overline{C+D}</math> | |||
!<math>p+\overline{B}</math> | |||
!<math>\overline{A}B</math> | |||
!<math>r \oplus q</math> | |||
!<math>s \oplus p</math> | |||
|- | |- | ||
|0 | |0 || 0 || 0 || 0 || 1 || 1 || 0 || 1 || 0 | ||
|0 | |||
| | |||
|0 | |||
|0 | |||
|1 | |||
|0 | |||
|1 | |||
| | |||
|- | |- | ||
|0 | |0 || 0 || 0 || 1 || 0 || 1 || 0 || 1 || 1 | ||
|0 | |||
|1 | |||
| | |||
|0 | |||
|1 | |||
|0 | |||
|1 | |||
|1 | |||
|- | |- | ||
|0 | |0 || 0 || 1 || 0 || 0 || 1 || 0 || 1 || 1 | ||
|1 | |||
|0 | |||
|0 | |||
|1 | |||
| | |||
|1 | |||
| | |||
|1 | |||
|- | |- | ||
|0 | |0 || 0 || 1 || 1 || 0 || 1 || 0 || 1 || 1 | ||
|1 | |||
|0 | |||
|1 | |||
|0 | |||
| | |||
|1 | |||
| | |||
|1 | |||
|- | |- | ||
|0 | |0 || 1 || 0 || 0 || 1 || 1 || 1 || 0 || 1 | ||
|1 | |||
| | |||
|0 | |||
|0 | |||
|1 | |||
|1 | |||
|1 | |||
|1 | |||
|- | |- | ||
|0 | |0 || 1 || 0 || 1 || 0 || 0 || 1 || 1 || 1 | ||
|1 | |||
|1 | |||
| | |||
|0 | |||
|0 | |||
|1 | |||
|1 | |||
|1 | |||
|- | |- | ||
|1 | |0 || 1 || 1 || 0 || 0 || 1 || 1 || 1 || 1 | ||
|0 | |||
|0 | |||
| | |||
|1 | |||
|1 | |||
| | |||
|1 | |||
| | |||
|- | |- | ||
|1 | |0 || 1 || 1 || 1 || 0 || 0 || 1 || 1 || 1 | ||
| | |||
|0 | |||
| | |||
|0 | |||
|1 | |||
| | |||
|1 | |||
|1 | |||
|- | |- | ||
|1 | |1 || 0 || 0 || 0 || 1 || 1 || 0 || 1 || 0 | ||
|0 | |||
| | |||
|0 | |||
|0 | |||
|1 | |||
|0 | |||
|1 | |||
| | |||
|- | |- | ||
|1 | |1 || 0 || 0 || 1 || 0 || 1 || 0 || 1 || 1 | ||
|0 | |||
|1 | |||
| | |||
|0 | |||
|1 | |||
|0 | |||
|1 | |||
|1 | |||
|- | |- | ||
|1 | |1 || 0 || 1 || 0 || 0 || 1 || 0 || 1 || 1 | ||
|1 | |||
|0 | |||
|0 | |||
|1 | |||
| | |||
|0 | |||
|1 | |||
| | |||
|- | |- | ||
|1 | |1 || 0 || 1 || 1 || 0 || 1 || 0 || 1 || 1 | ||
|1 | |||
|0 | |||
|1 | |||
|0 | |||
| | |||
| | |||
| | |||
| | |||
|- | |- | ||
|1 | |1 || 1 || 0 || 0 || 1 || 1 || 0 || 1 || 0 | ||
|1 | |||
| | |||
|0 | |||
|0 | |||
|0 | |||
| | |||
| | |||
|0 | |||
|- | |- | ||
|1 | |1 || 1 || 0 || 1 || 0 || 0 || 0 || 0 || 0 | ||
|1 | |- | ||
|1 | |1 || 1 || 1 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|1 | |- | ||
|0 | |1 || 1 || 1 || 1 || 0 || 0 || 0 || 0 || 0 | ||
|0 | |||
|0 | |||
|0 | |||
|0 | |||
|} | |} | ||
From the truth table, there are 10 rows where the final output is TRUE. | |||
== Sample Problem 3 == | == Sample Problem 3 == | ||
Simplify the | Simplify the Boolean expression that this circuit represents. | ||
[[File: | ::[[File:Circuit-PB.png|200px]] | ||
'''Solution:''' | '''Solution:''' | ||
The circuit translates as follows: | |||
<math>(\overline{A}(A+B))\overline{B+C}</math> | |||
<math>=(\overline{A}A+\overline{A}B)\overline{B}\overline{C}</math> | |||
<math>=(0+\overline{A}B)\overline{B}\overline{C}</math> | |||
<math>=\overline{A}B\overline{B}\overline{C}</math> | |||
<math>=0</math> | |||
= Video Resources = | = Video Resources = | ||
==ACSL Advisors== | |||
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads. | The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads. | ||
<!-- | <!-- | ||
| Line 388: | Line 302: | ||
--> | --> | ||
{| | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/gxil9VyGTtE</youtube> | |||
| [https://youtu.be/gxil9VyGTtE ''Digital Electronics -1'' ('''Ravi Yeluru (hemsra)''')] | |||
Introduces the AND, OR, and NOT gates, and works through a couple of simple circuits. | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/m7-wa5ca_G8</youtube> | |||
| [https://youtu.be/m7-wa5ca_G8 Digital Electronics -2'' ('''Ravi Yeluru (hemsra)''')] | |||
Solves a 3-gate circuit (the AND of an OR and a NOR) given by the Boolean expression <math>(\overline{A}+B)(\overline{B+C})</math>. | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/Eckd5UlJmB4</youtube> | |||
| [https://youtu.be/Eckd5UlJmB4 ''Digital Electronics Boolean Algebra'' ('''Tangerine Code''')] | |||
https://youtu.be/ | Solves a 3-gate circuit (the AND of an OR and a NOR) given by the Boolean expression | ||
<math>\overline{(A+B)}(B+C)</math>. | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/JJL6DsVCpHo</youtube> | |||
| [https://youtu.be/JJL6DsVCpHo ''ACSL Digital Electronics Worksheet Sample'' ('''misterminich''')] | |||
https://youtu.be/ | Solves a handful of ACSL problems. | ||
Logic Gate | |} | ||
Kevin Drumm | |||
==Other Videos== | |||
The topic of Digital Electronics is fundamental in Computer Science and there are many videos on YouTube that teach this subject. We found the following videos to be | |||
nice introductions to digital logic gates. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads. | |||
{| | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/s2MI_NgKD98</youtube> | |||
| [https://youtu.be/s2MI_NgKD98 ''Digital Electronics Basics'' ('''Beginning Electronics''')] | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/z9s8A8oBe7g</youtube> | |||
| [https://youtu.be/z9s8A8oBe7g ''Logic Gate Expressions'' ('''Kevin Drumm''')] | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/eroqZpbKrhc</youtube> | |||
| [https://youtu.be/eroqZpbKrhc ''Determining the truth table and logic statement'' ('''Anna does some physics''')] | |||
Uses a truth table to find the inputs that make the circuit <math>\not(A+B)+(AB)</math> true using a truth table. | |||
|} | |||
Latest revision as of 11:14, 18 December 2021
A digital circuit is constructed from logic gates. Each logic gate performs a function of boolean logic based on its inputs, such as AND or OR. Each circuit can be represented as a Boolean Algebra expression; this topic is an extension of the topic of Boolean Algebra, which includes a thorough description of truth tables and simplifying expressions.
Definitions
The following table illustrates all logic gates. For each logic gate, the table shows the equivalent Boolean algebra expression and truth table.
Note that there is some ambiguity in the conversion from a diagram to a circuit. For example, is [math]\overline{A+B}[/math] an OR gate followed by a NOT gate, or smply a NOT gate.
Online Tools
The Logisim application is a wonderful tool for exploring this topic. Logisim is free to download and use; among its many features is support to automatically draw a circuit from a Boolean Algebra expression; to simulate the circuit with arbitrary inputs; and to complete a truth table for the circuit. From the application, you can import the circuit corresponding to the Sample Problem 1 from the file located at http://www.acsl.org/misc/wiki-digital-electronics-sample1.circ. There are many YouTube videos that show how to use the Logisim application; including a very nice 4 minute tutorial.
Logisim contains many additional advanced features that are beyond the scope of ACSL problems.
Sample Problems
Sample Problem 1
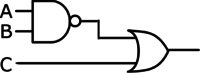
Find all ordered triplets (A, B, C) which make the following circuit FALSE:
Solution:
One approach to solving this problem is to reason about that inputs and outputs are necessary at each gate. For the circuit to be FALSE, both inputs to the file OR gate must be false. Thus, input C must be FALSE, and the output of the NAND gate must also be false. The NAND gate is false only when both of its inputs are TRUE; thus, inputs A and B must both be TRUE. The final answer is (TRUE, TRUE, FALSE), or (1, 1, 0).
Another approach to solving this problem is to translate the circuit into a Boolean Algebra expression and simplify the expression using the laws of Boolean Algebra. This circuit translates to the Boolean expression [math]\overline{AB}+C[/math]. To find when this is FALSE we can equivalently find when the [math]\overline{\overline{AB}+C}[/math] is TRUE. The expression becomes [math]\overline{\overline{AB}}\cdot \overline{C}[/math] after applying DeMorgan’s Law. The double NOT over the AB expression cancels out, to become [math]AB\overline{C}[/math]. The AND of 3 terms is TRUE when each term is TRUE, or A=1, B=1 and C=0.
Sample Problem 2
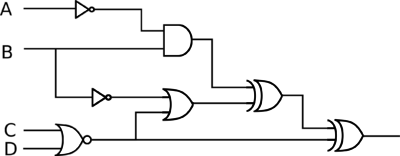
How many ordered 4-tuples (A, B, C, D) make the following circuit TRUE?
Solution:
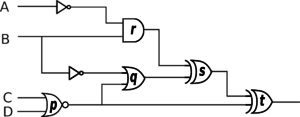
We'll use a truth table to solve this problem. The rows in the truth table will correspond to all possible inputs - 16 in this case, since there are 4 inputs. The output columns will be the output of each gate, other than the NOT gates. The diagram below labels each of the gates; it's useful to keep the column straight when working the truth table.
| INPUT | OUTPUT | |||||||
| A | B | C | D | p | q | r | s | t |
|---|---|---|---|---|---|---|---|---|
| [math]\overline{C+D}[/math] | [math]p+\overline{B}[/math] | [math]\overline{A}B[/math] | [math]r \oplus q[/math] | [math]s \oplus p[/math] | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
From the truth table, there are 10 rows where the final output is TRUE.
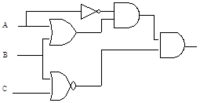
Sample Problem 3
Simplify the Boolean expression that this circuit represents.
Solution:
The circuit translates as follows:
[math](\overline{A}(A+B))\overline{B+C}[/math] [math]=(\overline{A}A+\overline{A}B)\overline{B}\overline{C}[/math] [math]=(0+\overline{A}B)\overline{B}\overline{C}[/math] [math]=\overline{A}B\overline{B}\overline{C}[/math] [math]=0[/math]
Video Resources
ACSL Advisors
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| Digital Electronics -1 (Ravi Yeluru (hemsra))
Introduces the AND, OR, and NOT gates, and works through a couple of simple circuits. | |
| Digital Electronics -2 (Ravi Yeluru (hemsra))
Solves a 3-gate circuit (the AND of an OR and a NOR) given by the Boolean expression [math](\overline{A}+B)(\overline{B+C})[/math]. | |
| Digital Electronics Boolean Algebra (Tangerine Code)
Solves a 3-gate circuit (the AND of an OR and a NOR) given by the Boolean expression [math]\overline{(A+B)}(B+C)[/math]. | |
| ACSL Digital Electronics Worksheet Sample (misterminich)
Solves a handful of ACSL problems. |
Other Videos
The topic of Digital Electronics is fundamental in Computer Science and there are many videos on YouTube that teach this subject. We found the following videos to be nice introductions to digital logic gates. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| Digital Electronics Basics (Beginning Electronics) | |
| Logic Gate Expressions (Kevin Drumm) | |
| Determining the truth table and logic statement (Anna does some physics)
Uses a truth table to find the inputs that make the circuit [math]\not(A+B)+(AB)[/math] true using a truth table. |