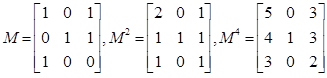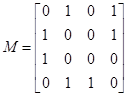Difference between revisions of "Graph Theory"

Latest revision as of 09:42, 23 September 2024

Many problems are naturally formulated in terms of points and connections between them. For example, a computer network has PCs connected by cables, an airline map has cities connected by routes, and a school has rooms connected by hallways. A graph is a mathematical object which models such situations.

Overview

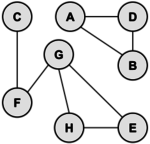
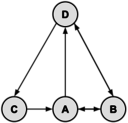
A graph is a collection of vertices and edges. An edge is a connection between two vertices (sometimes referred to as nodes). One can draw a graph by marking points for the vertices and drawing lines connecting them for the edges, but the graph is defined independently of the visual representation. For example, the following two drawings represent the same graph:

The precise way to represent this graph is to identify its set of vertices {A, B, C, D, E, F, G}, and its set of edges between these vertices {AB, AD, BD, CF, FG, GH, GE, HE}.

Terminology

The edges of the above graph have no directions meaning that the edge from one vertex A to another vertex B is the same as from vertex B to vertex A. Such a graph is called an undirected graph. Similarly, a graph having a direction associated with each edge is known as a directed graph.

A path from vertex x to y in a graph is a list of vertices, in which successive vertices are connected by edges in the graph. For example, FGHE is path from F to E in the graph above. A simple path is a path with no vertex repeated. For example, FGHEG is not a simple path.

A graph is connected if there is a path from every vertex to every other vertex in the graph. Intuitively, if the vertices were physical objects and the edges were strings connecting them, a connected graph would stay in one piece if picked up by any vertex. A graph which is not connected is made up of connected components. For example, the graph above has two connected components: {A, B, D} and {C, E, F, G, H}.

A cycle is a path, which is simple except that the first and last vertex are the same (a path from a point back to itself). For example, the path HEGH is a cycle in our example. Vertices must be listed in the order that they are traveled to make the path; any of the vertices may be listed first. Thus, HEGH and EHGE are different ways to identify the same cycle. For clarity, we list the start / end vertex twice: once at the start of the cycle and once at the end.

We’ll denote the number of vertices in a given graph by V and the number of edges by E. Graphs with all edges present are called complete graphs; graphs with relatively few edges present (say less than $V log(V)$) are called sparse; graphs with relatively few edges missing are called dense.

Directed Graphs

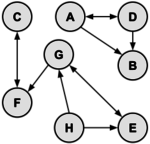
Directed graphs are graphs which have a direction associated with each edge. An edge xy in a directed graph can be used in a path that goes from x to y but not necessarily from y to x. For example, a directed graph similar to our example graph is drawn below:

This graph is defined as the set of vertices V = {A,B,C,D,E,F,G,H} and the set of edges {AB,AD,DA,DB,EG,GE,HG,HE,GF,CF,FC}. There is one directed path from G to C (namely, GFC); however, there are no directed paths from C to G. Note that a few of the edges have arrows on both ends, such as the edge between A and D. These dual arrows indicate that there is an edge in each direction, which essentially makes an undirected edge. An undirected graph can be thought of as a directed graph with all edges occurring in pairs in this way. A directed graph with no cycles is called a dag (directed acyclic graph).

Trees & Forests

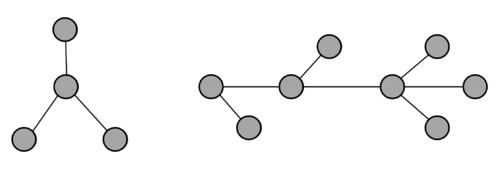
A graph with no cycles is called a tree. There is only one path between any two nodes in a tree. A tree with $N$ vertices contains exactly $N-1$ edges.

The two graphs shown above are trees because neither has any cycles and all vertices are connected. The graph on the left has 4 vertices and 3 edges; the graph on the right has 8 vertices and 7 edges. Note that in both cases, because they are trees, the number of edges is one less than the number of vertices.

A group of disconnected trees is called a forest.

A weighted graph is a graph that has a weight (also referred to as a cost) associated with each edge. For example, in a graph used by airlines where cities are vertices and edges are cities with direct flights connecting them, the weight for each edge might be the distance between the cities.

A spanning tree of a graph is a subgraph that contains all the vertices and forms a tree. A minimal spanning tree can be found for weighted graphs in order to minimize the cost across an entire network.

Adjacency Matrices

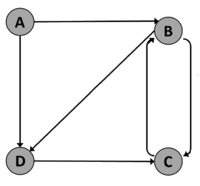
It is frequently convenient to represent a graph by a matrix known as an adjacency matrix. Consider the following directed graph:

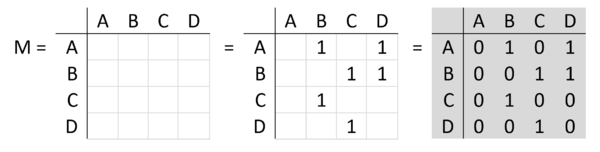
To draw the adjacency matrix, we create an $N$ by $N$ grid and label the rows and columns for each vertex (diagram at the left). Then, place a 1 for each edge in the cell whose row and column correspond to the starting and ending vertices of the edge (diagram in the middle). Finally, place a 0 in all other cells (diagram at the right).

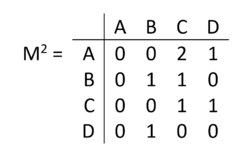
By construction, cell $(i,j)$ in the matrix with a value of 1 indicates a direct path from vertex $i$ to vertex $j$. If we square the matrix, the value in cell $(i,j)$ indicates the number of paths of length 2 from vertex $i$ to vertex $j$.

For example, the $M^2$ says that there 2 paths of length 2 from A to C (A → B → C and A → D → C). This also says that there is exactly 1 path of length 2 from A to D (A → B → D), exactly 1 path of length 2 from B to B (B → C → B), and so on.

In general, if we raise $M$ to the pth power, the resulting matrix indicates which paths of length $p$ exist in the graph. The value in $M^p(i,j)$ is the number of paths from vertex $i$ to vertex $j$.

Sample Problems

Problem 1

Find the number of different cycles contained in the directed graph with vertices {A, B, C, D, E} and edges {AB, BA, BC, CD, DC, DB, DE}.

Solution: The graph is as follows:

By inspection, the cycles are: ABA, BCDB, and CDC. Thus, there are 3 cycles in the graph.

Problem 2

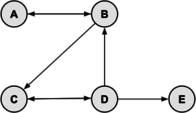
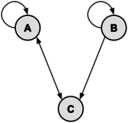
In the following directed graph, find the total number of different paths from vertex A to vertex C of length 2 or 4.

Solution:

Let matrix $M$ represent the graph. Recall that the number of paths from vertex $i$ to vertex $j$ of length $p$ equals $M^p[i,j]$. The values of $M$, $M^2$ and $M^4$ are:

There is 1 path of length 2 from A to C (cell [1,3] in $M^2$). By inspection, the only path of length 2 is A → A → C.

There are 3 paths of length 4 (cell [1,3] in $M^4$) and they are A → A → A → A → C, A → A → C → A → C, A → C → A → A → C.

Problem 3

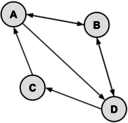
Given the adjacency matrix, draw the directed graph.

Solution:

There must be exactly 4 vertices: V = {A, B, C, D}. There must be be exactly 7 edges: E = {AB, AD, BA, BD, CA, DB, DC}. Here are two valid drawings of the graph:

Video Resources

ACSL Videos

The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.

	ACSL Math: Graph Theory (Raj Joshi) This video introduces the topic, then using an example problem, explains the methodology to solve problems that appear on ACSL contests.
	ACSL - Graph Theory Worksheet 1 (misterminich) Shows the solution to the ACSL problem: 'Draw the directed graph with vertices A, B, C, D, E and the directed edges AB, BC, AD, BC, DC, ED, and EA.
	ACSL Graph Theory Worksheet 3 (misterminich) Shows the solution to an ACSL problem asking to find how many paths of a specific length there are in a specific directed graph.
	Graph Theory ACSL Example Problem (Tangerine Code) Shows the solution to an ACSL problem asking to find how many different cycles there are from a specific vertex in a specific directed graph.

ACSL Test Prep - Graph Theory (Mrs. Goopta)

A talked-over presentation discussing graph theory as needed for the American Computer Science League and its tests.

@@ Line 11: / Line 11: @@
 == Terminology ==
-The edges of the above graph has no directions meaning the edge from one vertex A to another vertex B is the same as from vertex B to vertex A. So the graph above is an ''undirected graph''. Similarly graphs having a direction associated with each edge is known as ''directed graph'' (see section below).
+The edges of the above graph have no directions meaning that the edge from one vertex A to another vertex B is the same as from vertex B to vertex A. Such a graph is called an ''undirected graph''. Similarly, a graph having a direction associated with each edge is known as a ''directed graph''.
 A ''path'' from vertex x to y in a graph is a list of vertices, in which successive vertices are connected by edges in the graph.  For example, FGHE is path from F to E in the graph above.  A ''simple path'' is a path with no vertex repeated.  For example, FGHEG is not a simple path.
@@ Line 19: / Line 19: @@
 A ''cycle'' is a path, which is simple except that the first and last vertex are the same (a path from a point back to itself).  For example, the path HEGH is a cycle in our example.  Vertices must be listed in the order that they are traveled to make the path; any of the vertices may be listed first.  Thus, HEGH and EHGE are different ways to identify the same cycle.  For clarity, we list the start / end vertex twice: once at the start of the cycle and once at the end.
-We’ll denote the number of vertices in a given graph by V and the number of edges by E.  Note that E can range anywhere from V to V<sup>2</sup> (or V(V-1)/2 in an undirected graph).  Graphs with all edges present are called ''complete graphs''; graphs with relatively few edges present (say less than V log(V)) are called ''sparse''; graphs with relatively few edges missing are called ''dense.''
+We’ll denote the number of vertices in a given graph by V and the number of edges by E. Graphs with all edges present are called ''complete graphs''; graphs with relatively few edges present (say less than $V log(V)$) are called ''sparse''; graphs with relatively few edges missing are called ''dense.''
 == Directed Graphs ==
@@ Line 29: / Line 29: @@
 This graph is defined as the set of vertices V = {A,B,C,D,E,F,G,H} and the set of edges {AB,AD,DA,DB,EG,GE,HG,HE,GF,CF,FC}.  There is one directed path from G to C (namely, GFC); however, there are no directed paths from C to G.  Note that a few of the edges have arrows on both ends, such as the edge between A and D.  These dual arrows indicate that there is an edge in each direction, which essentially makes an undirected edge.  An ''undirected graph'' can be thought of as a directed graph with all edges occurring in pairs in this way.  A directed graph with no cycles is called a ''dag'' (directed acyclic graph).
-== Trees & Forest ==
+== Trees & Forests ==
-A graph with no cycles is called a ''tree''.  There is only one path between any two nodes in a tree.  A tree on N vertices contains exactly N-1 edges.
+A graph with no cycles is called a ''tree''.  There is only one path between any two nodes in a tree.  A tree with $N$ vertices contains exactly $N-1$ edges.
 [[File:forest.png|500px]]
-The graph on the left shown above is a tree because it has no cycles and vertices are connected.  It has four vertices and three edges, i.e., for ''N'' vertices ''N-1'' edges as mentioned in the definition.
+The two graphs shown above are trees because neither has any cycles and all vertices are connected. The graph
+on the left has 4 vertices and 3 edges; the graph on the right has 8 vertices and 7 edges. Note that in both cases, because they
+are trees,
+the number of edges is one less than the number of vertices.
-A ''spanning tree'' of a graph is a subgraph that contains all the vertices and forms a tree.  Minimal spanning trees can be found for weighted graphs (i.e. each edge has a cost or distance associated with it) in order to minimize the cost or distance across an entire network.
+A group of disconnected trees is called a ''forest''.
-A group of disconnected trees is called a ''forest''.
+A ''weighted graph'' is a graph that has a weight (also referred to as a cost) associated with each edge.
+For example, in a graph
+used by airlines where cities are vertices and edges are cities with direct flights connecting them,
+the weight for each edge might be the distance between the cities.
+A ''spanning tree'' of a graph is a subgraph that contains all the vertices and forms a tree.
+A ''minimal spanning tree''
+can be found for weighted graphs
+in order to minimize the cost across an entire network.
 == Adjacency Matrices ==
-It is frequently convenient to represent a graph by a matrix, as shown in the second sample problem below.  If we consider vertex A as 1, B as 2, etc., then a “one” in M at row ''i'' and column ''j'' indicates that there is an edge from vertex ''i'' to ''j''., whereas a "zero" indicates there is not an edge. If we raise M to the ''pth'' power, the resulting matrix indicates which paths of length ''p'' exist in the graph.  The value in $M^p(i,j)$ is the number of paths from vertex ''i'' to vertex ''j''.
+It is frequently convenient to represent a graph by a matrix known as an ''adjacency matrix.''  Consider
+the following directed graph:
+[[File:DirectedGraph.png|200px]]
-It is frequently convenient to represent a graph by a matrix known as Adjacency Matrix. Let us understand using the 4 node directed graph below:
+To draw the adjacency matrix, we create an $N$ by $N$ grid and label the rows and columns for each vertex (diagram at the left). Then, place a 1 for each edge in the cell whose row and column correspond to the
+starting and ending vertices of the edge (diagram in the middle). Finally, place
+a 0 in all other cells (diagram at the right).
-[[File:DirectedGraph.png|250px]]
+[[File:AdjMatrix.png|600px]]
-To draw adjacency matrix, we put all nodes in rows and also arrange them in columns which gives a 4x4 matrix (the left empty matrix). We then put 1 for all the edges considering their direction (see the middle one) and finally put 0 for all unfilled cells which gives us the adjacency matrix (the rightmost one, highlighted).
+By construction, cell $(i,j)$ in the matrix with a value of 1 indicates a direct path from vertex $i$ to vertex $j$.
+If we square the
+matrix, the value in cell $(i,j)$ indicates the number of paths of length 2 from vertex $i$ to vertex $j$.
-[[File:AdjMatrix.png]|200px]
+[[File:AdjMatrix2.png|250px]]
-Bu construction, each path of this matrix is of length 1. Now if we raise the power of matrix M to 2, we get:
+For example, the $M^2$ says that there 2 paths of length 2 from A to C (A → B → C and A → D → C).  This also says that there is exactly 1 path of length 2 from A to D (A → B → D), exactly 1 path of length 2 from B to B (B → C → B), and so on.
-[[File:AdjMatrix2.png|300px]]
+In general, if we raise $M$ to the ''pth'' power, the resulting matrix indicates which paths of length $p$ exist in the graph.
+The value in $M^p(i,j)$ is the number of paths from vertex $i$ to vertex $j$.
-And this says that there are 2 paths of length 2 from A to C. By examination we can see they are A->B->C and A->D->C. This also says that there is exactly 1 path of length 2 from A to D which is A->B->D, exactly 1 path of length 2 from B to B which is B->c->B and so on.
 == Sample Problems ==
@@ Line 104: / Line 120: @@
 [[File:matrix_s3.png]]
-There is 1 path of length 2 from A to C (cell [1,3] in $M^2$).  By inspection, the only path of length 2 is A->A->C.
+There is 1 path of length 2 from A to C (cell [1,3] in $M^2$).  By inspection, the only path of length 2 is A → A → C.
-There are 3 paths of length 4 (cell [1,3] in $M^4$) and they are A->A->A->A->C, A->A->C->A->C, A->C->A->A->C.
+There are 3 paths of length 4 (cell [1,3] in $M^4$) and they are A → A → A → A → C, A → A → C → A → C, A → C → A → A → C.
 === Problem 3 ===
@@ Line 163: / Line 179: @@
 {|
-|-
-| <youtube width="300" height="180">https://youtu.be/44sQJK4BycY</youtube>
-| [https://youtu.be/44sQJK4BycY ''CS 106B Lecture: Graphs: basic concepts'']
-This lecture from Stanford University is s wonderful introduction to graph theory. The lecture starts out with many examples of real world problems that are modeled by graphs, and then moves on to review basic terminology relating to graph theory.
 |-
 | <youtube width="300" height="180"> https://youtu.be/gXgEDyodOJU</youtube>