Difference between revisions of "Data Structures"
Marc Brown (talk | contribs) (→Trees) |
|||
| (32 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
This category concentrates on four of the most basic structures: '''stacks''', '''queues''', '''binary search trees''', and '''priority queues'''. Questions will cover these data structures and implicit algorithms, not specific to implementation language details. | This category concentrates on four of the most basic structures: '''stacks''', '''queues''', '''binary search trees''', and '''priority queues'''. Questions will cover these data structures and implicit algorithms, not specific to implementation language details. | ||
A ''stack'' is usually used to save information that will need to be processed later. Items are processed in a “last-in, first-out” (LIFO) order. A ''queue'' is usually used to process items in the order in which requests are generated; a new item is not processed until all items currently on the queue are processed. This is also known as “first-in, first-out” (FIFO) order. A ''binary search tree'' is used when one is storing | A ''stack'' is usually used to save information that will need to be processed later. Items are processed in a “last-in, first-out” (LIFO) order. A ''queue'' is usually used to process items in the order in which requests are generated; a new item is not processed until all items currently on the queue are processed. This is also known as “first-in, first-out” (FIFO) order. A ''binary search tree'' is used when one is storing items and needs to be able to efficiently process the operations of insertion, deletion, and query (i.e. find out if a particular item is found in the list of items and if not, which item is close to the item in question). A ''priority queue'' is used like a binary search tree, except one cannot delete an arbitrary item, nor can one make an arbitrary query. One can only find out or delete the smallest element of the list. | ||
There are many online resources covering these basic data structures; | There are many online resources covering these basic data structures; indeed there are many books and entire courses devoted to fundamental data structures. Implementation varies by computer language, but for our purposes, they can all be represented as a list of items that might contain duplicates. The rest of this page is an overview of these structures. | ||
== Stacks and Queues == | == Stacks and Queues == | ||
A ''stack'' supports two operations: PUSH and POP. A command of the form | A ''stack'' supports two operations: PUSH and POP. A command of the form PUSH("A") puts the key "A" at the top of the stack; the command “X = POP()” removes the top item from the stack and stores its value into variable X. If the stack was empty (because nothing had ever been pushed on it, or if all elements have been popped off of it), then X is given the special value of NIL. An analogy to this is a stack of books on a desk: a new book is placed on the top of the stack (pushed) and a book is removed from the top also (popped). Some textbooks call this data structure a “push-down stack” or a “LIFO stack”. | ||
''Queues'' operate just like stacks, except items are removed from the bottom instead of the top. A good physical analogy of this is the way a train conductor or newspaper boy uses a coin machine to give change: new coins are added to the tops of the piles, and change is given from the bottom of each. Some textbooks refer to this data structure as a “FIFO stack”. | ''Queues'' operate just like stacks, except items are removed from the bottom instead of the top. A command of the form PUSH("A") puts the key "A" at the top of the queue; the command “X = POP()” removes the item from the bottom of the queue and stores its value into variable X. If the queue was empty (because nothing had ever been pushed on it, or if all elements have been popped off of it), then X is given the special value of NIL. A good physical analogy of this is the way a train conductor or newspaper boy uses a coin machine to give change: new coins are added to the tops of the piles, and change is given from the bottom of each. Sometimes the top and bottom of a queue are referred to as the rear and the front respectively. Therefore, items are pushed/enqueued at the rear of the queue and popped/dequeued at the front of the queue. There is a similarity to the Britsh "queueing up". Some textbooks refer to this data structure as a “FIFO stack”. | ||
Consider the following sequence of 14 operations: | Consider the following sequence of 14 operations: | ||
< | <pre> | ||
PUSH("A") | |||
PUSH("M") | |||
PUSH("E") | |||
X = POP() | |||
PUSH("R") | |||
X = POP() | |||
PUSH("I") | |||
X = POP() | |||
X = POP() | |||
X = POP() | |||
X = POP() | |||
PUSH("C") | |||
PUSH("A") | |||
PUSH("N") | |||
</pre> | |||
If these operations are applied to a stack, then the values of the pops are: E, R, I, M, A and NIL. After all of the operations, there are three items still on the stack: the N is at the top (it will be the next to be popped, if nothing else is pushed before the pop command), and C is at the bottom. If, instead of using a stack we used a queue, then the values popped would be: A, M, E, R, I and NIL. There would be three items still on the queue: N at the top and C on the bottom. Since items are removed from the bottom of a queue, C would be the next item to be popped regardless of any additional pushes. | |||
=== Pre-2018 Syntax === | |||
ACSL Contests pre-2018 used a slightly different, and more liberal, syntax. Consider the following sequence on a stack: | |||
<pre> | |||
PUSH(A) | PUSH(A) | ||
PUSH( | PUSH(B) | ||
PUSH( | PUSH(C) | ||
POP(X) | POP(X) | ||
POP(Z) | |||
POP( | </pre> | ||
After the 5 operations, the stack would be left with A as the only element on the stack, the value of C in variable X, and the value of B in variable Z. | |||
Were the above operations applied to a queue, the queue would be left with C; variable X would contain A; and variable Z would contain B. | |||
== Trees == | == Trees == | ||
| Line 42: | Line 58: | ||
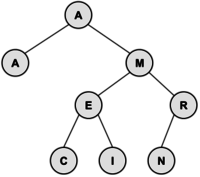
The following tree is built from the keys A, M, E, R, I, C, A, N in that order: | The following tree is built from the keys A, M, E, R, I, C, A, N in that order: | ||
[[File: | <center> | ||
[[File:bst-american.svg|200px]] | |||
</center> | |||
The ''root'' of the resulting tree is the node containing the key A | The ''root'' of the resulting tree is the node containing the key A. Our ACSL convention places duplicate keys into the tree as if they were less than their equal key. (In some textbooks and software libraries, duplicate keys may be considered larger than their equal key.) The tree has a ''depth'' (sometimes called height) of 3 because the deepest node is 3 nodes below the root. The root node has a depth of 0. Nodes with no children are called leaf nodes; there are four of them in the tree: A, C, I and N. Our ACSL convention is that an ''external node'' is the name given to a place where a new node could be attached to the tree. (In some textbooks, an external node is synonymous with a leaf node.) In the final tree above, there are 9 external nodes; these are not drawn. The tree has an ''internal path length'' of 15 which is the sum of the depths of all nodes. It has an ''external path length'' of 31 which is the sum of the depths of all external nodes. To insert the N (the last key inserted), 3 ''comparisons'' were needed against the root A (>), the M (>), and the R (≤). | ||
To perform an ''inorder'' traversal of the tree, recursively traverse the tree by first visiting the left child, then the root, then the right child. In the tree above, the nodes are visited in the following order: A, A, C, E, I, M, N, and R. A ''preorder'' travel (root, left, right) visits in the following order: A, A, M, E, C, I, R, and N. A ''postorder'' traversal (left, right, root) is: A, C, I, E, N, R, M, A. Inorder traversals are typically used to list the contents of the tree in sorted order. | To perform an ''inorder'' traversal of the tree, recursively traverse the tree by first visiting the left child, then the root, then the right child. In the tree above, the nodes are visited in the following order: A, A, C, E, I, M, N, and R. A ''preorder'' travel (root, left, right) visits in the following order: A, A, M, E, C, I, R, and N. A ''postorder'' traversal (left, right, root) is: A, C, I, E, N, R, M, A. Inorder traversals are typically used to list the contents of the tree in sorted order. | ||
A binary search tree can support the operations insert, delete, and search. Moreover, it handles the operations efficiently for ''balanced'' trees. In a tree with 1 million items, one can search for a particular value in about log<sub>2</sub> 1,000,000 ≈ 20 steps. Items can be inserted or deleted in about as many steps, too. However, consider the binary search tree resulting from inserting the keys A, E, I, O, U, Y which places all of the other letters on the right side of the root "A". This is very unbalanced; therefore, sophisticated algorithms can be used to maintain balanced trees. Binary search trees are “dynamic” data structures that can support many operations in any order and introduces or removes nodes as needed. | |||
To search for a node in a binary tree, the following algorithm (in pseudo-code) is used: | To search for a node in a binary tree, the following algorithm (in pseudo-code) is used: | ||
<syntaxhighlight> | <syntaxhighlight lang="text"> | ||
p = root | p = root | ||
found = FALSE | found = FALSE | ||
while (p ≠ NIL) and (not found) | while (p ≠ NIL) and (not found) | ||
if (x<p’s key) | if (x < p’s key) | ||
p = p’s left child | p = p’s left child | ||
else if (x>p’s key) | else if (x > p’s key) | ||
p = p’s right child | p = p’s right child | ||
else | else | ||
| Line 68: | Line 86: | ||
Deleting from a binary search tree is a bit more complicated. The algorithm we’ll use is as follows: | Deleting from a binary search tree is a bit more complicated. The algorithm we’ll use is as follows: | ||
<syntaxhighlight> | <syntaxhighlight lang="text"> | ||
p = node to delete | p = node to delete | ||
f = father of p | f = father of p | ||
| Line 87: | Line 105: | ||
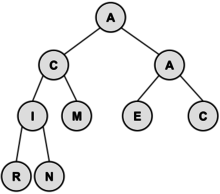
These diagrams illustrate the algorithm using the tree above. At the left, we delete I (0 children); in the middle, we delete the R (1 child); and at the right, we delete the M (2 children). | These diagrams illustrate the algorithm using the tree above. At the left, we delete I (0 children); in the middle, we delete the R (1 child); and at the right, we delete the M (2 children). | ||
<center> | |||
{| class ="wikitable" | {| class ="wikitable" | ||
|[[File: | |[[File:bst-american-del-i.svg|200px]] | ||
|[[File: | |[[File:bst-american-del-r.svg|200px]] | ||
|[[File: | |[[File:bst-american-del-m.svg|200px]] | ||
|} | |} | ||
</center> | |||
There are also general trees that use the same terminology, but they have 0 or more ''subnodes'' which can be accessed with an array or linked list of pointers. ''Pre-order'' and ''post-order'' traversals are possible with these trees, but the other algorithms do not work in the same way. Applications of general trees include game theory, organizational charts, family trees, etc. | There are also general trees that use the same terminology, but they have 0 or more ''subnodes'' which can be accessed with an array or linked list of pointers. ''Pre-order'' and ''post-order'' traversals are possible with these trees, but the other algorithms do not work in the same way. Applications of general trees include game theory, organizational charts, family trees, etc. | ||
| Line 99: | Line 119: | ||
== Priority Queues == | == Priority Queues == | ||
A ''priority queue'' is quite similar to a binary search tree, but one can only delete the smallest item and | A ''priority queue'' is quite similar to a binary search tree, but one can only delete the smallest item and retrieve the smallest item only. These insert and delete operations can be done in a guaranteed time proportional to the log (base 2) of the number of items; the retrieve-the-smallest can be done in constant time. | ||
The | The standard way to implement a priority queue is using a ''heap'' data structure. A heap uses a binary tree (that is, a tree with two children) and maintains the following two properties: every node is less than or equal to both of its two children (nothing is said about the relative magnitude of the two children), and the resulting tree contains no “holes”. That is, all levels of the tree are completely filled, except the bottom level, which is filled in from the left to the right. | ||
The algorithm for insertion is not too difficult: put the new node at the bottom of the tree and then go up the tree, making exchanges with its parent, until the tree is valid. | |||
<!--here would be the place to show building the heap with AMERICAN--> | |||
The heap at the left | |||
was building from the letters A, M, E, R, I, C, A, N (in that order); the heap at the right is after a C has been added. | |||
The smallest value is always the root. To delete it (and one can only delete the smallest value), one replaces it with the bottom-most and right-most element, and then walks down the tree making exchanges with the child in order to | <center> | ||
{| class="wikitable" | |||
|[[File:heap-american.svg|220px]]|| | |||
[[File:heap-american-insert-c.svg|220px]] | |||
|} | |||
</center> | |||
The smallest value is always the root. To delete it (and one can only delete the smallest value), one replaces it with the bottom-most and right-most element, and then walks down the tree making exchanges with the smaller child in order to ensure that the tree is valid. The following pseudo-code formalizes this notion: | |||
<syntaxhighlight> | <syntaxhighlight lang="text"> | ||
b = bottom-most and right-most element | b = bottom-most and right-most element | ||
p = root of tree | p = root of tree | ||
| Line 118: | Line 148: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
When the smallest item is at the root of the heap, the heap is called a ''min-heap''. Of course, A ''max-heap'' is also possible and is common in practice. An efficient implementation of a heap uses an array that can be understood conceptually by using a tree data structure. | |||
== Sample Problems == | == Sample Problems == | ||
=== | === Problem 1 === | ||
Consider an initially empty stack. | Consider an initially empty stack. After the following operations are performed, what is the value of Z? | ||
<syntaxhighlight lang="text"> | |||
3 6 8 | PUSH(3) | ||
PUSH(6) | |||
PUSH(8) | |||
Y = POP() | |||
X = POP() | |||
PUSH(X-Y) | |||
Z = POP() | |||
</syntaxhighlight> | |||
= | '''Solution:''' The first POP stores 8 in Y. The second POP stores 6 in X. Then, 6-8=-2 is pushed onto the stack. Finally, the last POP removes the -2 and stores it in Z. | ||
=== Problem 2 === | |||
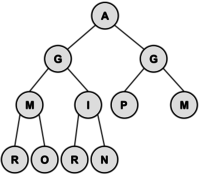
Create a min-heap with the letters in the word PROGRAMMING. What are the letters in the bottom-most row, from left to right? | |||
'''Solution:''' The bottom row contains the letters RORN, from left-to-right. Here is the entire heap: | |||
<center> | |||
[[File:heap-programming.svg|200px]] | |||
</center> | |||
=== Problem 3 === | |||
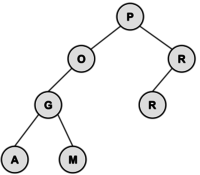
Create a binary search tree from the letters in the word PROGRAM. What is the internal path length? | |||
= | '''Solution:''' When drawing the tree, P has a depth of 0, O and R have a depth of 1, G and R have a depth of 2, and A and M have a depth of 3. Therefore, the internal path length is 2*1 + 2*2 + 2*3 = 12. Here is the tree: | ||
<center> | |||
[[File:bst-program.svg|200px]] | |||
</center> | |||
= Video Resources = | = Video Resources = | ||
| Line 187: | Line 215: | ||
Shows how to build a binary search tree from the letters '''S U S H I'''. | Shows how to build a binary search tree from the letters '''S U S H I'''. | ||
|- | |- | ||
| <youtube width="300" height="180">https://youtu.be/l9aMO7lgHj0</youtube> | | <youtube width="300" height="180">https://youtu.be/l9aMO7lgHj0</youtube> | ||
| Line 192: | Line 221: | ||
A general tutorial on internal path length of a binary search tree | A general tutorial on internal path length of a binary search tree | ||
|- | |||
| <youtube width="300" height="180">https://youtu.be/Olu_RbWnHb8</youtube> | |||
| [https://youtu.be/Olu_RbWnHb8 ''ACSL Test Prep - Data Structures - Queues, Stacks, Binary Search Trees, and Heaps'' ('''Mrs. Gupta''')] | |||
A talked-over presentation discussing queues, stacks, binary search trees, and heaps as needed for the American Computer Science League and its tests. | |||
|} | |} | ||
== Other Videos == | == Other Videos == | ||
There is no shortage of instructional video material covering basic data structures. Here is a series that | There is no shortage of instructional video material covering basic data structures. Here is a series that combines teaching concepts with showing Java code that implements the concepts. Most of the ACSL questions will not involve coding the basic operations on the data structures; rather, the problems will involve high-level understanding of them. However, seeing the code is an excellent way to thoroughly understand these data structures, and what it takes to implement them. | ||
{| | {| | ||
|- | |||
| <youtube width="300" height="180">https://youtu.be/wjI1WNcIntg</youtube> | |||
| [https://youtu.be/wjI1WNcIntg ''Data Structures: Stacks and Queues'' ('''HackerRank''')] | |||
The first half of the video is a nice description of stacks and queues; the second half walks through very clean Java code that implements the fundamental methods on these data structures. | |||
|- | |- | ||
| <youtube width="300" height="180">https://youtu.be/njTh_OwMljA</youtube> | | <youtube width="300" height="180">https://youtu.be/njTh_OwMljA</youtube> | ||
| Line 203: | Line 243: | ||
Although ACSL does not cover linked lists per se, they are a great preliminary study for binary search trees. | Although ACSL does not cover linked lists per se, they are a great preliminary study for binary search trees. | ||
|- | |- | ||
| <youtube width="300" height="180">https://youtu.be/oSWTXtMglKE</youtube> | | <youtube width="300" height="180">https://youtu.be/oSWTXtMglKE</youtube> | ||
| [https://youtu.be/oSWTXtMglKE ''Data Structures: Trees'' ('''HackerRank''')] | | [https://youtu.be/oSWTXtMglKE ''Data Structures: Trees'' ('''HackerRank''')] | ||
Learn | Learn about binary search trees. This video is a part of HackerRank's ''Cracking The Coding Interview Tutorial'' with Gayle Laakmann McDowell. The first half of the video is a clear and eloquent description of binary search trees; the second half walks through very clean Java code that implements the fundamental methods. | ||
|- | |- | ||
| <youtube width="300" height="180">https://youtu.be/t0Cq6tVNRBA</youtube> | | <youtube width="300" height="180">https://youtu.be/t0Cq6tVNRBA</youtube> | ||
| [https://youtu.be/t0Cq6tVNRBA ''Data Structures: Heaps'' ('''HackerRank''')] | | [https://youtu.be/t0Cq6tVNRBA ''Data Structures: Heaps'' ('''HackerRank''')] | ||
Learn about heaps. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is | Learn about heaps. This video is a part of HackerRank's ''Cracking The Coding Interview Tutorial'' with Gayle Laakmann McDowell. The first half of the video is a clear and eloquent description of heaps; the second half walks through very clean Java code that implements the fundamental methods. | ||
|} | |||
Here are a few more videos covering the basics of binary search trees. | |||
{| | |||
|- | |||
| <youtube width="300" height="180">https://youtu.be/FvdPo8PBQtc</youtube> | |||
| [https://youtu.be/FvdPo8PBQtc ''How to Construct a Binary Search Tree'' ('''edutechional''')] | |||
''In this algorithm tutorial, I walk through how to construct a binary search tree given an unordered array, and then how to find elements inside of the tree.'' | |||
|} | |} | ||
Latest revision as of 22:43, 9 June 2020
At the heart of virtually every computer program are its algorithms and its data structures. It is hard to separate these two items, for data structures are meaningless without algorithms to create and manipulate them, and algorithms are usually trivial unless there are data structures on which to operate. The bigger the data sets, the more important data structures are in various algorithms.
This category concentrates on four of the most basic structures: stacks, queues, binary search trees, and priority queues. Questions will cover these data structures and implicit algorithms, not specific to implementation language details.
A stack is usually used to save information that will need to be processed later. Items are processed in a “last-in, first-out” (LIFO) order. A queue is usually used to process items in the order in which requests are generated; a new item is not processed until all items currently on the queue are processed. This is also known as “first-in, first-out” (FIFO) order. A binary search tree is used when one is storing items and needs to be able to efficiently process the operations of insertion, deletion, and query (i.e. find out if a particular item is found in the list of items and if not, which item is close to the item in question). A priority queue is used like a binary search tree, except one cannot delete an arbitrary item, nor can one make an arbitrary query. One can only find out or delete the smallest element of the list.
There are many online resources covering these basic data structures; indeed there are many books and entire courses devoted to fundamental data structures. Implementation varies by computer language, but for our purposes, they can all be represented as a list of items that might contain duplicates. The rest of this page is an overview of these structures.
Stacks and Queues
A stack supports two operations: PUSH and POP. A command of the form PUSH("A") puts the key "A" at the top of the stack; the command “X = POP()” removes the top item from the stack and stores its value into variable X. If the stack was empty (because nothing had ever been pushed on it, or if all elements have been popped off of it), then X is given the special value of NIL. An analogy to this is a stack of books on a desk: a new book is placed on the top of the stack (pushed) and a book is removed from the top also (popped). Some textbooks call this data structure a “push-down stack” or a “LIFO stack”.
Queues operate just like stacks, except items are removed from the bottom instead of the top. A command of the form PUSH("A") puts the key "A" at the top of the queue; the command “X = POP()” removes the item from the bottom of the queue and stores its value into variable X. If the queue was empty (because nothing had ever been pushed on it, or if all elements have been popped off of it), then X is given the special value of NIL. A good physical analogy of this is the way a train conductor or newspaper boy uses a coin machine to give change: new coins are added to the tops of the piles, and change is given from the bottom of each. Sometimes the top and bottom of a queue are referred to as the rear and the front respectively. Therefore, items are pushed/enqueued at the rear of the queue and popped/dequeued at the front of the queue. There is a similarity to the Britsh "queueing up". Some textbooks refer to this data structure as a “FIFO stack”.
Consider the following sequence of 14 operations:
PUSH("A")
PUSH("M")
PUSH("E")
X = POP()
PUSH("R")
X = POP()
PUSH("I")
X = POP()
X = POP()
X = POP()
X = POP()
PUSH("C")
PUSH("A")
PUSH("N")
If these operations are applied to a stack, then the values of the pops are: E, R, I, M, A and NIL. After all of the operations, there are three items still on the stack: the N is at the top (it will be the next to be popped, if nothing else is pushed before the pop command), and C is at the bottom. If, instead of using a stack we used a queue, then the values popped would be: A, M, E, R, I and NIL. There would be three items still on the queue: N at the top and C on the bottom. Since items are removed from the bottom of a queue, C would be the next item to be popped regardless of any additional pushes.
Pre-2018 Syntax
ACSL Contests pre-2018 used a slightly different, and more liberal, syntax. Consider the following sequence on a stack:
PUSH(A) PUSH(B) PUSH(C) POP(X) POP(Z)
After the 5 operations, the stack would be left with A as the only element on the stack, the value of C in variable X, and the value of B in variable Z.
Were the above operations applied to a queue, the queue would be left with C; variable X would contain A; and variable Z would contain B.
Trees
Trees, in general, use the following terminology: the root is the top node in the tree; children are the nodes that are immediately below a parent node; leaves are the bottom-most nodes on every branch of the tree; and siblings are nodes that have the same immediate parent.
A binary search tree is composed of nodes having three parts: information (or a key), a pointer to a left child, and a pointer to a right child. It has the property that the key at every node is always greater than or equal to the key of its left child, and less than the key of its right child.
The following tree is built from the keys A, M, E, R, I, C, A, N in that order:
The root of the resulting tree is the node containing the key A. Our ACSL convention places duplicate keys into the tree as if they were less than their equal key. (In some textbooks and software libraries, duplicate keys may be considered larger than their equal key.) The tree has a depth (sometimes called height) of 3 because the deepest node is 3 nodes below the root. The root node has a depth of 0. Nodes with no children are called leaf nodes; there are four of them in the tree: A, C, I and N. Our ACSL convention is that an external node is the name given to a place where a new node could be attached to the tree. (In some textbooks, an external node is synonymous with a leaf node.) In the final tree above, there are 9 external nodes; these are not drawn. The tree has an internal path length of 15 which is the sum of the depths of all nodes. It has an external path length of 31 which is the sum of the depths of all external nodes. To insert the N (the last key inserted), 3 comparisons were needed against the root A (>), the M (>), and the R (≤).
To perform an inorder traversal of the tree, recursively traverse the tree by first visiting the left child, then the root, then the right child. In the tree above, the nodes are visited in the following order: A, A, C, E, I, M, N, and R. A preorder travel (root, left, right) visits in the following order: A, A, M, E, C, I, R, and N. A postorder traversal (left, right, root) is: A, C, I, E, N, R, M, A. Inorder traversals are typically used to list the contents of the tree in sorted order.
A binary search tree can support the operations insert, delete, and search. Moreover, it handles the operations efficiently for balanced trees. In a tree with 1 million items, one can search for a particular value in about log2 1,000,000 ≈ 20 steps. Items can be inserted or deleted in about as many steps, too. However, consider the binary search tree resulting from inserting the keys A, E, I, O, U, Y which places all of the other letters on the right side of the root "A". This is very unbalanced; therefore, sophisticated algorithms can be used to maintain balanced trees. Binary search trees are “dynamic” data structures that can support many operations in any order and introduces or removes nodes as needed.
To search for a node in a binary tree, the following algorithm (in pseudo-code) is used:
p = root
found = FALSE
while (p ≠ NIL) and (not found)
if (x < p’s key)
p = p’s left child
else if (x > p’s key)
p = p’s right child
else
found = TRUE
end if
end while
Deleting from a binary search tree is a bit more complicated. The algorithm we’ll use is as follows:
p = node to delete
f = father of p
if (p has no children)
delete p
else if (p has one child)
make p’s child become f’s child
delete p
else if (p has two children)
l = p’s left child (it might also have children)
r = p’s right child (it might also have children)
make l become f’s child instead of p
stick r onto the l tree
delete p
end if
These diagrams illustrate the algorithm using the tree above. At the left, we delete I (0 children); in the middle, we delete the R (1 child); and at the right, we delete the M (2 children).
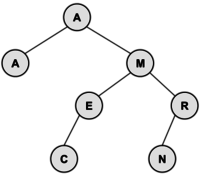
|
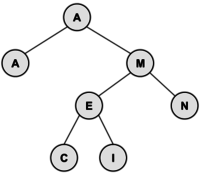
|
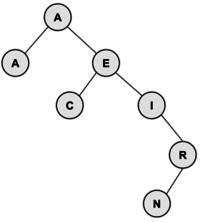
|
There are also general trees that use the same terminology, but they have 0 or more subnodes which can be accessed with an array or linked list of pointers. Pre-order and post-order traversals are possible with these trees, but the other algorithms do not work in the same way. Applications of general trees include game theory, organizational charts, family trees, etc.
Balanced trees minimize searching time when every leaf node has a depth of within 1 of every other leaf node. Complete trees are filled in at every level and are always balanced. Strictly binary trees ensure that every node has either 0 or 2 subnodes. You may want to consider how there are exactly 5 strictly binary trees with 7 nodes.
Priority Queues
A priority queue is quite similar to a binary search tree, but one can only delete the smallest item and retrieve the smallest item only. These insert and delete operations can be done in a guaranteed time proportional to the log (base 2) of the number of items; the retrieve-the-smallest can be done in constant time.
The standard way to implement a priority queue is using a heap data structure. A heap uses a binary tree (that is, a tree with two children) and maintains the following two properties: every node is less than or equal to both of its two children (nothing is said about the relative magnitude of the two children), and the resulting tree contains no “holes”. That is, all levels of the tree are completely filled, except the bottom level, which is filled in from the left to the right.
The algorithm for insertion is not too difficult: put the new node at the bottom of the tree and then go up the tree, making exchanges with its parent, until the tree is valid. The heap at the left was building from the letters A, M, E, R, I, C, A, N (in that order); the heap at the right is after a C has been added.
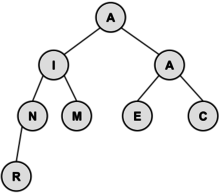 |
The smallest value is always the root. To delete it (and one can only delete the smallest value), one replaces it with the bottom-most and right-most element, and then walks down the tree making exchanges with the smaller child in order to ensure that the tree is valid. The following pseudo-code formalizes this notion:
b = bottom-most and right-most element
p = root of tree
p’s key = b’s key
delete b
while (p is larger than either child)
exchange p with smaller child
p = smaller child
end while
When the smallest item is at the root of the heap, the heap is called a min-heap. Of course, A max-heap is also possible and is common in practice. An efficient implementation of a heap uses an array that can be understood conceptually by using a tree data structure.
Sample Problems
Problem 1
Consider an initially empty stack. After the following operations are performed, what is the value of Z?
PUSH(3)
PUSH(6)
PUSH(8)
Y = POP()
X = POP()
PUSH(X-Y)
Z = POP()
Solution: The first POP stores 8 in Y. The second POP stores 6 in X. Then, 6-8=-2 is pushed onto the stack. Finally, the last POP removes the -2 and stores it in Z.
Problem 2
Create a min-heap with the letters in the word PROGRAMMING. What are the letters in the bottom-most row, from left to right?
Solution: The bottom row contains the letters RORN, from left-to-right. Here is the entire heap:
Problem 3
Create a binary search tree from the letters in the word PROGRAM. What is the internal path length?
Solution: When drawing the tree, P has a depth of 0, O and R have a depth of 1, G and R have a depth of 2, and A and M have a depth of 3. Therefore, the internal path length is 2*1 + 2*2 + 2*3 = 12. Here is the tree:
Video Resources
ACSL Videos
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| Data Structures (Stacks and Queues) (Tangerine Code)
A general tutorial on stacks and queues. | |
| Construct a Binary Search Tree (Tangerine Code)
Shows how to build a binary search tree from the letters S U S H I. | |
| Binary Search Tree ACSL Problem (Internal Path Length) (Tangerine Code)
A general tutorial on internal path length of a binary search tree | |
| ACSL Test Prep - Data Structures - Queues, Stacks, Binary Search Trees, and Heaps (Mrs. Gupta)
A talked-over presentation discussing queues, stacks, binary search trees, and heaps as needed for the American Computer Science League and its tests. |
Other Videos
There is no shortage of instructional video material covering basic data structures. Here is a series that combines teaching concepts with showing Java code that implements the concepts. Most of the ACSL questions will not involve coding the basic operations on the data structures; rather, the problems will involve high-level understanding of them. However, seeing the code is an excellent way to thoroughly understand these data structures, and what it takes to implement them.
| Data Structures: Stacks and Queues (HackerRank)
The first half of the video is a nice description of stacks and queues; the second half walks through very clean Java code that implements the fundamental methods on these data structures. | |
| Data Structures: Linked Lists (HackerRank)
Although ACSL does not cover linked lists per se, they are a great preliminary study for binary search trees. | |
| Data Structures: Trees (HackerRank)
Learn about binary search trees. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is a clear and eloquent description of binary search trees; the second half walks through very clean Java code that implements the fundamental methods. | |
| Data Structures: Heaps (HackerRank)
Learn about heaps. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is a clear and eloquent description of heaps; the second half walks through very clean Java code that implements the fundamental methods. |
Here are a few more videos covering the basics of binary search trees.
| How to Construct a Binary Search Tree (edutechional)
In this algorithm tutorial, I walk through how to construct a binary search tree given an unordered array, and then how to find elements inside of the tree. |