Difference between revisions of "FSAs and Regular Expressions"
Marc Brown (talk | contribs) |
Marc Brown (talk | contribs) m (capitalized Regular Expression throughout) |
||
| Line 6: | Line 6: | ||
= Basics = | = Basics = | ||
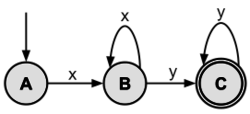
Here is a drawing of an FSA that is used to parse strings | Here is a drawing of an FSA that is used to parse strings consisting of x's and y's: | ||
<center> | <center> | ||
| Line 14: | Line 14: | ||
In the above FSA, there are three states: A, B, and C. The initial state is A; the final state is C. The only way to go from state A to B is by ''seeing'' the letter x. Once in state B, there are two transition rules: Seeing the letter y will cause the FSA to make C the active state, and seeing an x will keep B as the active state. State C is a final state, so if the string being parsed is completed and the FSA is in State C, the input string is said to be ''accepted'' by the FSA. In State C, seeing any additional letter y will keep the machine in state C. The FSA above will accept strings composed of one or more x’s followed by one or more y’s (e.g., xy, xxy, xxxyy, xyyy, xxyyyy). | In the above FSA, there are three states: A, B, and C. The initial state is A; the final state is C. The only way to go from state A to B is by ''seeing'' the letter x. Once in state B, there are two transition rules: Seeing the letter y will cause the FSA to make C the active state, and seeing an x will keep B as the active state. State C is a final state, so if the string being parsed is completed and the FSA is in State C, the input string is said to be ''accepted'' by the FSA. In State C, seeing any additional letter y will keep the machine in state C. The FSA above will accept strings composed of one or more x’s followed by one or more y’s (e.g., xy, xxy, xxxyy, xyyy, xxyyyy). | ||
Just like [[Boolean Algebra]] is a convenient algebraic representation of [[Digital Electronics]] Circuits, a | Just like [[Boolean Algebra]] is a convenient algebraic representation of [[Digital Electronics]] Circuits, a Regular Expression (RE) is an algebraic representation of an FSA. For example, the regular expression corresponding to the first FSA given above is xx*yy*. | ||
The rules for forming a | The rules for forming a Regular Expression (RE) are as follows: | ||
:1. The null string (λ) is a RE. | :1. The null string (λ) is a RE. | ||
:2. If the string a is in the input alphabet, then it is a RE. | :2. If the string a is in the input alphabet, then it is a RE. | ||
| Line 24: | Line 24: | ||
::c. CLOSURE. “a*” (a repeated zero or more times). This is known as the Kleene Star. | ::c. CLOSURE. “a*” (a repeated zero or more times). This is known as the Kleene Star. | ||
Identities for | Identities for Regular Expressions appear in the next section. The order of precedence for Regular Expression operators is: Kleene Star, concatenation, and then union. | ||
If we have a | If we have a Regular Expression, then we can mechanically build an FSA to accept the strings which are generated by the Regular Expression. Conversely, if we have an FSA, we can mechanically develop a Regular Expression which will describe the strings which can be parsed by the FSA. For a given FSA or Regular Expression, there are many others which are equivalent to it. A “most simplified” Regular Expression or FSA is not always well defined. | ||
<!-- | <!-- | ||
Most programming languages today have a package to handle Regular Expressions in order to do pattern matching algorithms more easily. Visual BASIC has the LIKE operator that is very easy to use. We will use these “basic” symbols in our category description. | Most programming languages today have a package to handle Regular Expressions in order to do pattern matching algorithms more easily. Visual BASIC has the LIKE operator that is very easy to use. We will use these “basic” symbols in our category description. | ||
| Line 77: | Line 77: | ||
--> | --> | ||
Typical problems in the category will include: translate an FSA to a | Typical problems in the category will include: translate an FSA to a Regular Expression; simplify a Regular Expression; determine which Regular Expressions or FSAs are equivalent; and determine which strings are accepted by either an FSA or a Regular Expression. | ||
= Regular Expression Identities = | = Regular Expression Identities = | ||
| Line 104: | Line 104: | ||
== Problem 1 == | == Problem 1 == | ||
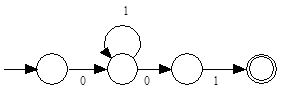
Find a simplified | Find a simplified Regular Expression for the following FSA: | ||
[[File:fsa_s1.png]] | [[File:fsa_s1.png]] | ||
| Line 114: | Line 114: | ||
== Problem 2 == | == Problem 2 == | ||
Which of the following strings are accepted by the following | Which of the following strings are accepted by the following Regular Expression "00*1*1U11*0*0" ? | ||
::A. 0000001111111 | ::A. 0000001111111 | ||
Revision as of 23:47, 11 September 2018
A Finite State Automaton (FSA) is a mathematical model of computation comprising: a finite number of states, of which exactly one is active at any given time; transition rules to change the active state; an initial state; and one more final states. We can draw an FSA by representing each state as a circle; the final state as a double circle; the start state as the only state with an incoming arrow; and the transition rules as labeled-edges connecting the states. When labels are assigned to states, they appear inside the circle representing the state.
In this category, FSAs will be limited to parsing strings. That is, determining if a string is valid or not.
Basics
Here is a drawing of an FSA that is used to parse strings consisting of x's and y's:
In the above FSA, there are three states: A, B, and C. The initial state is A; the final state is C. The only way to go from state A to B is by seeing the letter x. Once in state B, there are two transition rules: Seeing the letter y will cause the FSA to make C the active state, and seeing an x will keep B as the active state. State C is a final state, so if the string being parsed is completed and the FSA is in State C, the input string is said to be accepted by the FSA. In State C, seeing any additional letter y will keep the machine in state C. The FSA above will accept strings composed of one or more x’s followed by one or more y’s (e.g., xy, xxy, xxxyy, xyyy, xxyyyy).
Just like Boolean Algebra is a convenient algebraic representation of Digital Electronics Circuits, a Regular Expression (RE) is an algebraic representation of an FSA. For example, the regular expression corresponding to the first FSA given above is xx*yy*.
The rules for forming a Regular Expression (RE) are as follows:
- 1. The null string (λ) is a RE.
- 2. If the string a is in the input alphabet, then it is a RE.
- 3. if the strings a and b are both REs, then so are the strings built up using the following rules:
- a. CONCATENATION. “ab” (a followed by b).
- b. UNION. “aUb” (a or b).
- c. CLOSURE. “a*” (a repeated zero or more times). This is known as the Kleene Star.
Identities for Regular Expressions appear in the next section. The order of precedence for Regular Expression operators is: Kleene Star, concatenation, and then union.
If we have a Regular Expression, then we can mechanically build an FSA to accept the strings which are generated by the Regular Expression. Conversely, if we have an FSA, we can mechanically develop a Regular Expression which will describe the strings which can be parsed by the FSA. For a given FSA or Regular Expression, there are many others which are equivalent to it. A “most simplified” Regular Expression or FSA is not always well defined.
Typical problems in the category will include: translate an FSA to a Regular Expression; simplify a Regular Expression; determine which Regular Expressions or FSAs are equivalent; and determine which strings are accepted by either an FSA or a Regular Expression.
Regular Expression Identities
| 1. (a*)* = a* |
| 2. aa* = a*a |
| 3. aa* U λ = a* |
| 4. a(b U c) = ab U ac |
| 5. a(ba)* = (ab)*a |
| 6. (a U b)* = (a* U b*)* |
| 7. (a U b)* = (a*b*)* |
| 8. (a U b)* = a*(ba*)* |
Sample Problems
Problem 1
Find a simplified Regular Expression for the following FSA:
Solution:
The expression 01*01 is read directly from the FSA. It is in its most simplified form.
Problem 2
Which of the following strings are accepted by the following Regular Expression "00*1*1U11*0*0" ?
- A. 0000001111111
- B. 1010101010
- C. 1111111
- D. 0110
- E. 10
Solution:
Choice A uses the left hand pattern (00*1*1) and choice E uses the right hand pattern (11*0*0). Every string must start and end in the opposite digit so choices C and D don’t work. Choice B doesn’t work because all 1s and all 0s must be together. The correct answer is A and E.
Problem 3
Which, if any, of the following Regular Expressions are equivalent?
- A. (aUb)(ab*)(b*Ua)
- B. (aab*Ubab*)a
- C. aab*Ubab*UaabaUbab*a
- D. aab*Ubab*Uaab*aUbab*a
- E. a*Ub*
Solution:
Choice B can be discarded because it is the only RE whose strings must end with an a. Choice E can be discarded since it is the only RE that can accept a null string. Choices C and D are not equal. After expanding choice A, we must compare it to choices C and D. It is equal to choice D, but not to choice C. The only REs that are equivalent are choices A and D.
Video Resources
Nice two-part video showing the relationship between FSAs and REs.
| 1 - Convert Regular Expression to Finite-State Automaton (Barry Brown) | |
| 2 - Convert Regular Expression to Finite-State Automaton (Barry Brown)
This video uses the symbol "+" to mean "1 or more matches of the previous term". For example, "ab+" is the same as "abb*". |